Hard-Margin SVM: Primal Formulation
Optimization Problem:
$$
\min_{w, b} \quad \frac{1}{2} \|w\|^2 \\
\text{subject to} \quad y_i(w^\top x_i + b) \geq 1, \quad \forall i
$$
- Maximizes the margin between two classes
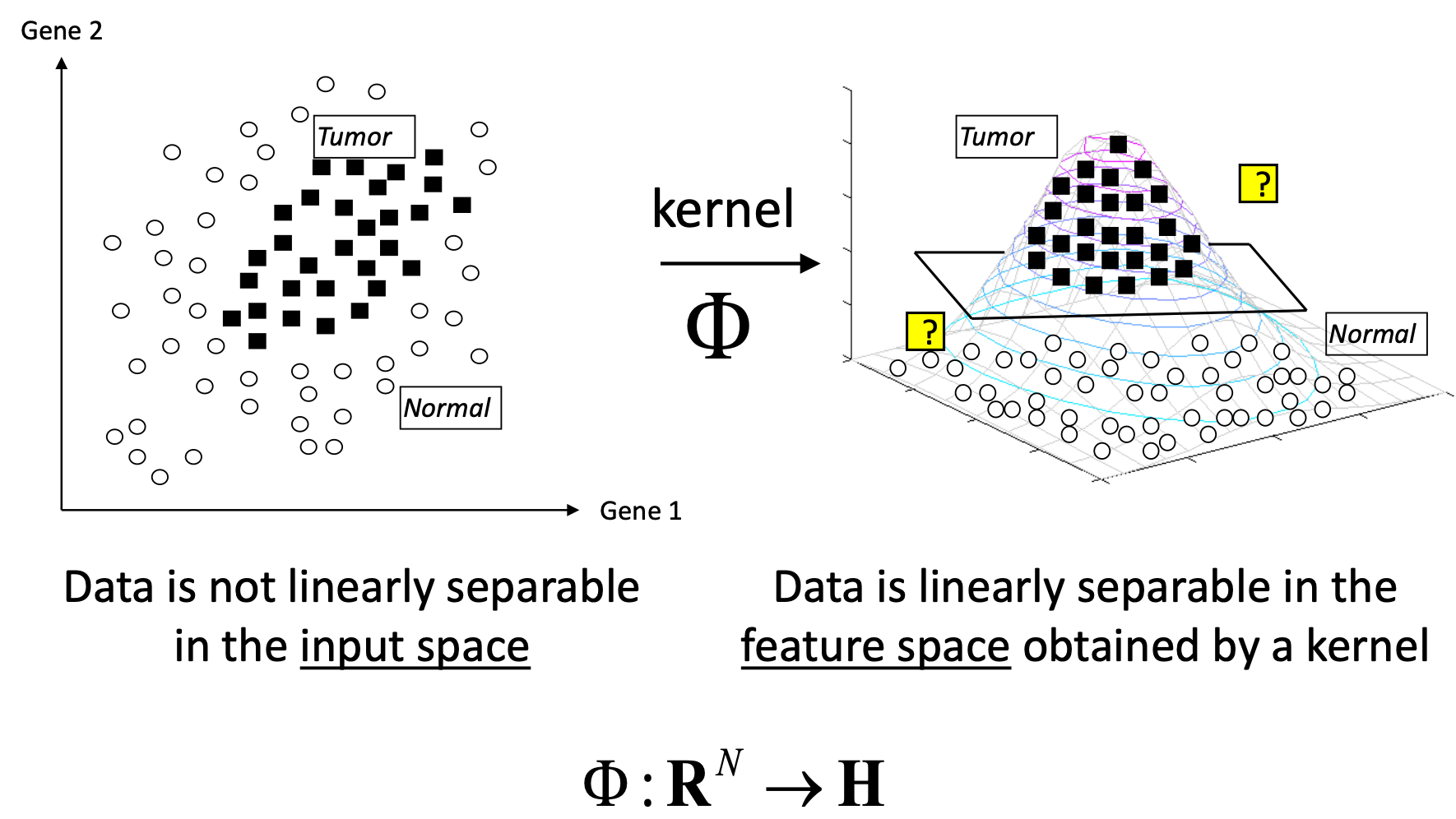
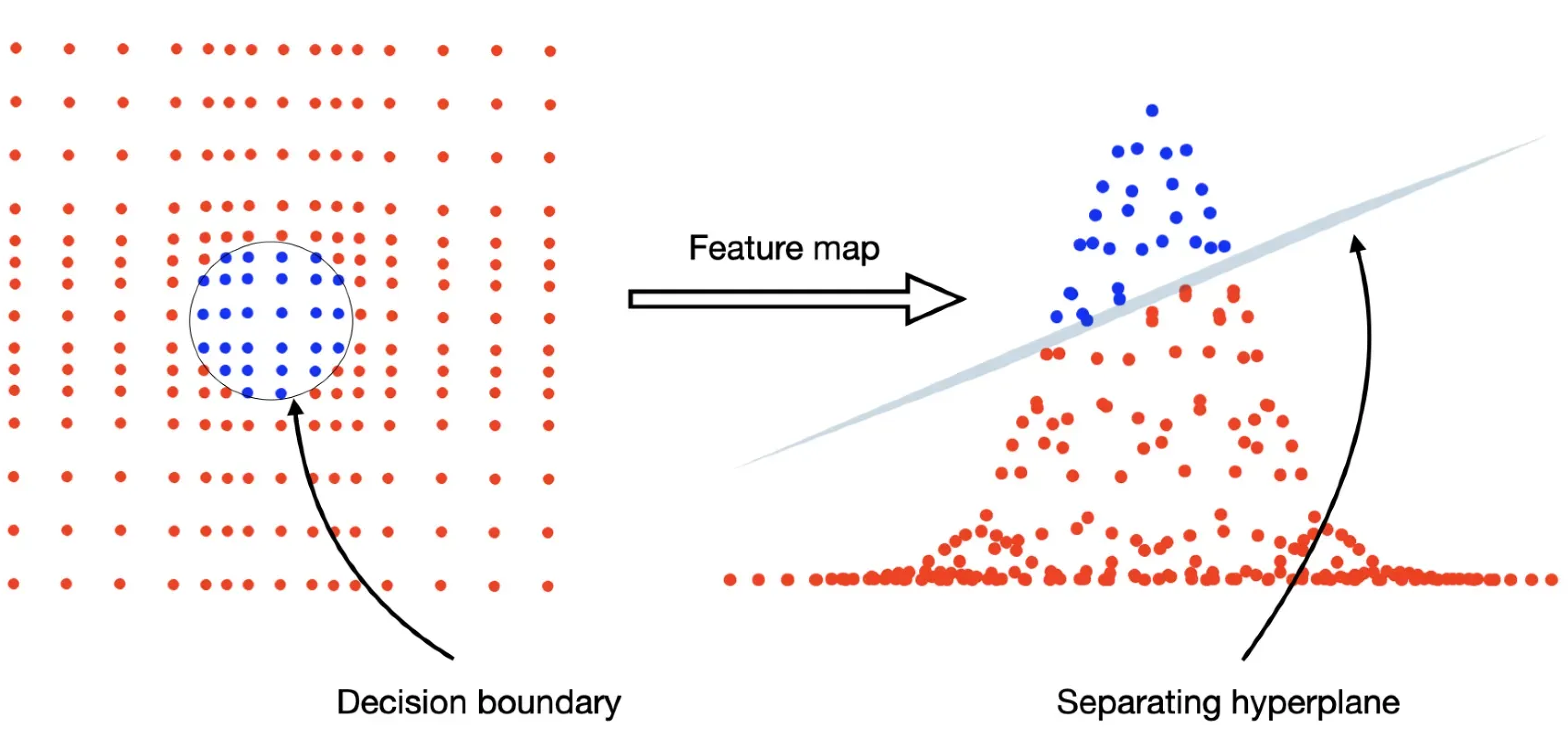
- Assumes data is linearly separable
Why Min-Max via Lagrangian?
Constrained optimization problems can be converted into a Lagrangian saddle-point problem:
$$
\min_{w, b} \max_{\alpha \geq 0} \mathcal{L}(w, b, \alpha)
$$
- Inequality constraints are incorporated using Lagrange multipliers $\alpha_i \geq 0$
- The Lagrangian combines the objective and constraints:
$$
\mathcal{L}(w, b, \alpha) = \frac{1}{2} \|w\|^2 - \sum_{i=1}^N \alpha_i \left[ y_i(w^\top x_i + b) - 1 \right]
$$
- The min-max structure reflects the game between minimizing the primal and maximizing the dual feasibility.
Game-Theoretic Interpretation of Duality
Why a Game?
Min-max two-player zero-sum game where one player (the "optimizer") minimizes an objective function, while the other player (the "constraint enforcer") maximizes a penalty term related to constraint violations.
- In the Lagrangian form:
$$
\min_{w, b} \max_{\alpha \geq 0} \mathcal{L}(w, b, \alpha)
$$
there is a natural interpretation as a two-player zero-sum game.
- Player 1 (Primal): chooses $ (w, b) $ to minimize the original primal cost (margin$^{-1}$).
- Player 2 (Dual): chooses $ \alpha $ to maximize the penalty for constraint violations.